Question

Please help, with an explanation !!

Answer 1

Ratio remains same

• AX:XC=DX:XB=3:2

So

• DX=12cm
• XB=8cm
• AX=7.2cm
• XC=4.8cm

Now

<ABX be P

`\\ \rm\Rrightarrow tanP=(AX)/(BX)`

`\\ \rm\Rrightarrow tanP=(7.2)/(8)`

`\\ \rm\Rrightarrow tanP=(9)/(10)`

`\\ \rm\Rrightarrow P=41.98°`

And

• <XBC be N

`\\ \rm\Rrightarrow tanN=(XC)/(BX)`

`\\ \rm\Rrightarrow tanN=(4.8)/(8)=(3)/(5)`

`\\ \rm\Rrightarrow tanN=0.6`

`\\ \rm\Rrightarrow N=30.96`

Now

• <ABC=30.96+41.98=72.94°

Answer 2

∠ABC = 73.74° (nearest hundredth)

Explanation:

Properties of a kite:

• A kite has two pairs of equal sides.
• It has one pair of equal angles.
• The diagonals bisect at right angles

If X is the point of intersection, the length of BD = 20 cm
and DX : XB = 3 : 2, then

⇒ DX = 3/5 of 20 and XB = 2/5 of 20

⇒ DX = 12 cm and XB = 8 cm

(see attached diagram)

∠ABC =∠XBC + ∠XBA

As ∠XBC ≅ ∠XBA then ∠ABC = 2∠XBC

To find ∠XBC use tan ratio:

`\mathsf{tan(\theta)=(opposite \ side)/(adjacent \ side)}`

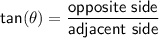
Given in ΔXBC

• angle = ∠XBC
• side opposite the angle = 6 cm
• side adjacent the angle = 8 cm

`\mathsf{tan(XBC)=(6)/(8)=\frac34}`

`\mathsf{angle(XBC)=tan^(-1)\left(\frac34\right)}`

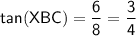
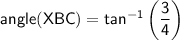
∠XBC = 36.86989765...°

Therefore, ∠ABC = 2 x 36.86989765...°

= 73.73979529...°

= 73.74° (nearest hundredth)