Question

(1 / 7 - 4√3)^3 + (1 / 7 + 4√3)^3

Answer 1

Given:

The expression is:

`\left((1)/(7)-4√(3)\right)^3+\left((1)/(7)+4√(3)\right)^3`

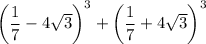
To find:

The simplified form of the given expression.

Solution:

Formulae used:

`(a-b)^3=a^3-3a^2b+3ab^2-b^3`

`(a-b)^3=a^3+3a^2b+3ab^2+b^3`

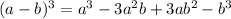
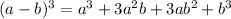
Adding this formulae, we get

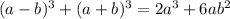`(a-b)^3+(a+b)^3=2a^3+6ab^2` ...(i)

We have,

`\left((1)/(7)-4√(3)\right)^3+\left((1)/(7)+4√(3)\right)^3`

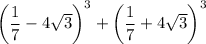
Using formula (i), the given expression can be written as:

`=2\left((1)/(7)\right)^3+6\left((1)/(7)\right)\left(4√(3)\right)^2`

`=2* (1)/(343)+6\left((1)/(7)\right)48`

`=(2)/(343)+(288)/(7)`

`=(2+14112)/(343)`

`=(14114)/(343)`

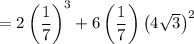
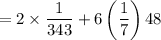
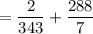
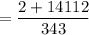
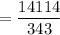
Therefore, the simplified form of the given expression is
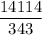`(14114)/(343)`.