Let's apply the derivative to both sides with respect to x. We'll use the chain rule.
![y = \ln\left(x + √(x^2+a^2)\right)\\\\\\(dy)/(dx) = (d)/(dx)\left[\ln\left(x + √(x^2+a^2)\right)\right]\\\\\\(dy)/(dx) = (1)/(x+√(x^2+a^2))*(d)/(dx)\left[x + √(x^2+a^2)\right]\\\\\\(dy)/(dx) = (1)/(x+(x^2+a^2)^(1/2))*\left(1 + 2x*(1)/(2)(x^2+a^2)^(-1/2)\right)\\\\\\(dy)/(dx) = (1)/(x+(x^2+a^2)^(1/2))*\left(1 + x*(1)/((x^2+a^2)^(1/2))\right)\\\\\\(dy)/(dx) = (1)/(x+W)*\left(1 + x*(1)/(W)\right)\\\\\\](https://img.qammunity.org/2022/formulas/mathematics/college/ght20utavmgxqiphmscf9sr3iv0gcoblas.png)
where W = (x^2+a^2)^(1/2) = sqrt(x^2+a^2)
Let's simplify that a bit.
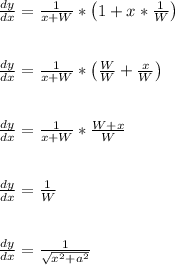
This concludes the first part of what your teacher wants.
-----------------------
Now onto the second part.
In this case, a = 3 so a^2 = 3^2 = 9.
Recall that if
![g(x) = (d)/(dx)\left[f(x)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/exhpa3i0noguvog796k2xrlbc7lov22jzh.png)
then

We can say that f(x) is the antiderivative of g(x). The C is some constant.
So,
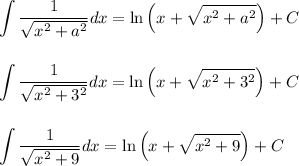
Now let g(x) = ln(x + sqrt(x^2+9) ) + C
Then compute
- g(0) = ln(3)+C
- g(4) = ln(9) = ln(3^2) = 2*ln(3)+C
Therefore,
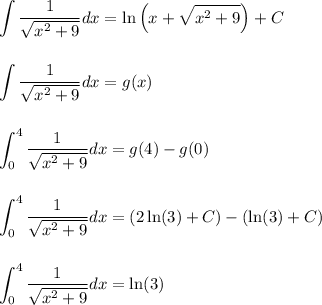
---------------------------------------
Extra info:
Interestingly, WolframAlpha says that the result is
 , but we can rewrite that into ln(3) because inverse hyperbolic sine is defined as
, but we can rewrite that into ln(3) because inverse hyperbolic sine is defined as
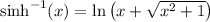
which is the function your teacher gave you, but now a = 1.
If you plugged x = 4/3 into the hyperbolic sine definition above, then you should get
