Answer:
∠ABC = 73.74° (nearest hundredth)
Explanation:
Properties of a kite:
- A kite has two pairs of equal sides.
- It has one pair of equal angles.
- The diagonals bisect at right angles
If X is the point of intersection, the length of BD = 20 cm
and DX : XB = 3 : 2, then
⇒ DX = 3/5 of 20 and XB = 2/5 of 20
⇒ DX = 12 cm and XB = 8 cm
(see attached diagram)
∠ABC =∠XBC + ∠XBA
As ∠XBC ≅ ∠XBA then ∠ABC = 2∠XBC
To find ∠XBC use tan ratio:
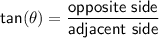
Given in ΔXBC
- angle = ∠XBC
- side opposite the angle = 6 cm
- side adjacent the angle = 8 cm
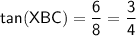
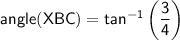
∠XBC = 36.86989765...°
Therefore, ∠ABC = 2 x 36.86989765...°
= 73.73979529...°
= 73.74° (nearest hundredth)