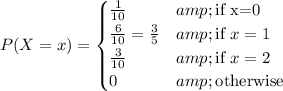Question

A committee of 3 is to be selected randomly from a group of 3 men and 2 women.

Let X represent the number of women on the committee. Find the probability
distribution of X.

Answer 1

Total number of ways to select 3 people from the 5 total: 5!/(3! (5 - 3)!) = 10

• Number of ways of picking 0 women:

`\dbinom20*\dbinom33 = 1*1 = 1`

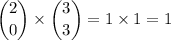
• Number of ways of picking 1 woman:

`\dbinom21*\dbinom32 = 2*3 = 6`

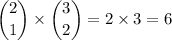
• Number of ways of picking 2 women:

`\dbinom22*\dbinom31 = 1*3 = 3`

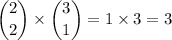
• Number of ways of picking 3 women: 0, since there are only 2 to choose from

Then X has the probability mass function

`P(X=x) = \begin{cases}\frac1{10}&\text{if x=0}\\\frac6{10}=\frac35&\text{if }x=1\\\frac3{10}&\text{if }x=2\\0&\text{otherwise}\end{cases}`