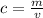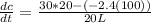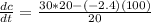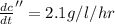Complete Question
A tank contains 100 grams of a substance dissolved in a large amount of water. The tank is filtered in such a way that water drains from the tank, leaving the substance behind in the tank. Consider the volume of the dissolved substance to be negligible. At what rate is the concentration (grams/liter) of the substance changing with respect to time in each scenario? (a) the rate after 5 hours, if the tank contains 60 L of water initially, and drains at a constant rate of 4 L/hr?
(b) the rate at the instant when 20 liters remain, if the water is draining at 2.4 L/hr at that instant g/L
c) the rate in scenario (b), if the unknown substance is also being added at a rate of 30 g/hr (and there are 100 grams in the tank at that instant)
Answer:
a)
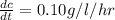
b)
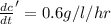
c)
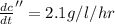
Step-by-step explanation:
From the question we are told that:
Mass m=100g
a)
Rate
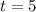
Volume
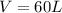

Generally the equation for Concentration is mathematically given by

Where
V=initial volume -(Drain Rate*time)
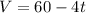
Therefore

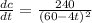
At t=5
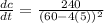
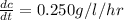
b)
Volume
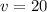
Rate
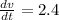
Generally the equation for Concentration is mathematically given by
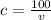
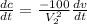
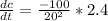
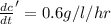
c)
Rate
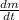
Generally the equation for Concentration is mathematically given by