Answer:
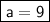
Explanation:
Two lines are given to us which are perpendicular to each other and we need to find out the value of a . The given equations are ,
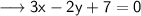
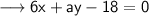
Step 1 : Convert the equations in slope intercept form of the line .
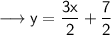
and ,
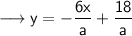
Step 2: Find the slope of the lines :-
Now we know that the product of slope of two perpendicular lines is -1. Therefore , from Slope Intercept Form of the line we can say that the slope of first line is ,
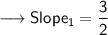
And the slope of the second line is ,
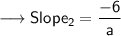
Step 3: Multiply the slopes :-
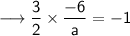
Multiply ,
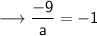
Multiply both sides by a ,
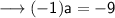
Divide both sides by -1 ,
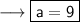
Hence the value of a is 9 .