Question

An capacitor consists of two large parallel plates of area A separated by a very small distance d. This capacitor is connected to a battery and charged until its plates carry charges Q and - Q, and then disconnected from the battery. If the separation between the plates is now doubled, the potential difference between the plates will

Answer 1

Will be doubled.

Step-by-step explanation:

For a capacitor of parallel plates of area A, separated by a distance d, such that the charges in the plates are Q and -Q, the capacitance is written as:

`C = (Q)/(V) = e_0(A)/(d)`

where e₀ is a constant, the electric permittivity.

Now we can isolate V, the potential difference between the plates as:

`V = (Q)/(e_0) *(d)/(A)`

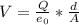
Now, notice that the separation between the plates is in the numerator.

Thus, if we double the distance we will get a new potential difference V', such that:

`V' = (Q)/(e_0) *(2d)/(A) = 2*( (Q)/(e_0) *(d)/(A)) = 2*V\\V' = 2*V`

So, if we double the distance between the plates, the potential difference will also be doubled.