Answer:
3) About 0.35 grams of hydrogen gas.
4) About 65.2 grams of aluminum oxide.
Step-by-step explanation:
Question 3)
We are given that 7.9 grams of sodium is dropped into a bathtub of water, and we want to determine how many grams of hydrogen gas is released.
Since sodium is higher than hydrogen on the activity series, sodium will replace hydrogen in a single-replacement reaction for sodium oxide. Hence, our equation is:
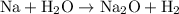
To balance it, we can simply add another sodium atom on the left. Hence:
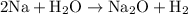
To convert from grams of sodium to grams of hydrogen gas, we can convert from sodium to moles of sodium, use the mole ratios to find moles in hydrogen gas, and then use hydrogen's molar mass to find its amount in grams.
The molar mass of sodium is 22.990 g/mol. Hence:
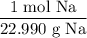
From the chemical equation, we can see that two moles of sodium produce one mole of hydrogen gas. Hence:
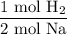
And the molar mass of hydrogen gas is 2.016 g/mol. Hence:
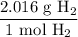
Given the initial value and the above ratios, this yields:
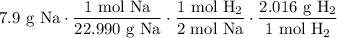
Cancel like units:
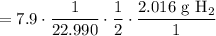
Multiply. Hence:
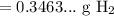
Since we should have two significant values:
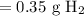
So, about 0.35 grams of hydrogen gas will be released.
Question 4)
Excess oxygen gas is added to 34.5 grams of aluminum and produces aluminum oxide. Hence, our chemical equation is:
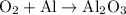
To balance this, we can place a three in front of the oxygen, four in front of aluminum, and two in front of aluminum oxide. Hence:
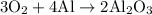
To convert from grams of aluminum to grams of aluminum oxide, we can convert aluminum to moles, use the mole ratios to find the moles of aluminum oxide, and then use its molar mass to determine the amount of grams.
The molar mass of aluminum is 26.982 g/mol. Thus:
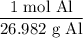
According to the equation, four moles of aluminum produces two moles of aluminum oxide. Hence:
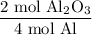
And the molar mass of aluminum oxide is 101.961 g/mol. Hence:
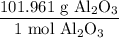
Using the given value and the above ratios, we acquire:
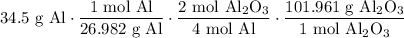
Cancel like units:
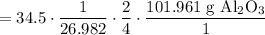
Multiply:
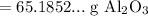
Since the resulting value should have three significant figures:
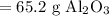
So, approximately 65.2 grams of aluminum oxide is produced.