Question

a mass of 10kg is suspended from the end of a steel rod of length 2m and radius 1mm. what is the elongation of the rod beyond its original length (Take E= 200 × 109^9 N/m²).​

Answer 1

ΔL = 3.12 x 10⁻⁴ m = 0.312 mm

Step-by-step explanation:

First, we will find the stress applied by the mass on the rod:

`\sigma = (F)/(A)`

where,

σ = stress = ?

F = Force applied by the mass = weight = mg = (10 kg)(9.81 m/s²) = 98.1 N

A = cross-sectional area = πr² = π(1 mm)² = π(0.001 m)² = 3.14 x 10⁻⁶ m²

Therefore,

`\sigma = (98.1\ N)/(3.14\ x\ 10^(-6)\ m^2)\\\\`

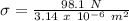
σ = 3.12 x 10⁷ Pa

Now, we will find the value of strain:

`E = (\sigma)/(\epsilon)\\\\\epsilon = (\sigma)/(E)\\\\\epsilon = (3.12\ x\ 10^7\ Pa)/(200\ x\ 10^9\ Pa)`

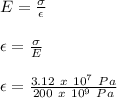
∈ = 1.56 x 10⁻⁴

Now, the change in length can be given by the formula of strain:

`\epsilon = (\Delta L)/(L)\\\\\Delta L = (\epsilon)(L)`

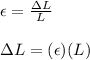
where,

L = Original Length = 2 m

ΔL = Elongation = ?

Therefore,

ΔL = (1.56 x 10⁻⁴)(2 m)

ΔL = 3.12 x 10⁻⁴ m = 0.312 mm