Given:
The function is:
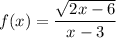
To find:
The smallest possible integer value for $x$ such that $f(x)$ has a real number value.
Solution:
We have,
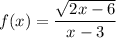
This function is defined if the radicand is greater than or equal to 0, i.e.,
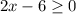 and the denominator is non-zero, i.e.,
and the denominator is non-zero, i.e.,
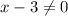 .
.
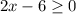
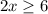
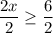
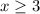 ...(i)
...(i)
And,
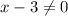
Adding 3 on both sides, we get

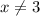 ...(ii)
...(ii)
Using (i) and (ii), it is clear that the function is defined for all real values which are greater than 3 but not 3.
Therefore, the smallest possible integer value for x is 4.