Question

A cone has a radius of 5 ft and a height of 15 ft. It is empty and is being filled with water at a constant rate of 24 ft 3 / sec . Find the rate of change of the radius of the surface of the water when the radius of the surface of the water is 2 ft. (You must also include the units)

Answer 1

The rate of change of the radius of the surface of the water when the radius of the surface of the water is 2 feet is approximately 0.637 feet per second.

Explanation:

The volume of the cone (
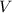`V`), in cubic feet, is defined by the following equation:

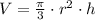`V = (\pi)/(3)\cdot r^(2)\cdot h` (1)

Where:

`r` - Radius, in feet.

`h` - Height, in feet.

And there is the following ratio of the radius to the height is:

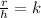`(r)/(h) = k` (2)

By applying (2) in (1):

`h = (r)/(k)`

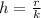
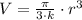`V = (\pi)/(3\cdot k)\cdot r^(3)` (3)

And the rate of change of the radius is found by differentiating on (3):

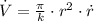`\dot V = (\pi)/(k)\cdot r^(2)\cdot \dot r` (4)

Where:

`\dot V` - Rate of change of the volume, in cubic feet per second.

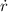`\dot r` - Rate of change of the surface of the water, in feet per second.

`\dot r = (k\cdot \dot V)/(\pi\cdot r^(2))`

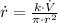
If we know that
`k = (1)/(3)`,
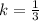`\dot V = 24\,(ft^(3))/(s)` and
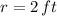`r = 2\,ft`, then the rate of change of the radius of the surface of the water is:

`\dot r = (\left((1)/(3) \right)\cdot \left(24\,(ft^(3))/(s) \right))/(\pi\cdot (2\,ft)^(2))`

`\dot r = 0.637\,(ft)/(s)`

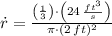
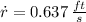
The rate of change of the radius of the surface of the water when the radius of the surface of the water is 2 feet is approximately 0.637 feet per second.