Solution :
A). x = 2 (mod 3)
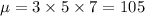
x = 3 (mod 5)
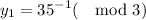
x = 4 (mod 7)
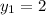
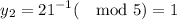
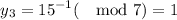
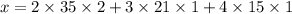
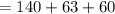
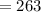
≡ 53(mod 105)
Hence the solution is 105 k + 53 > 1000 for k = 10
Therefore, the minimum number of students = 1103
B).
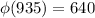
By Eulu's theory
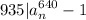 if n and 935 are coprime.
if n and 935 are coprime.
Now,
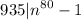 and 80 x 8 = 640
and 80 x 8 = 640
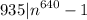 ⇒ g(n,935) = 1
⇒ g(n,935) = 1
⇒ 5, 11, 17 do not divide n