Question

In a large chemical factory, a feed pipe carries a liquid at a speed of 5.5 m/s. A pump pushes the liquid along at a gauge pressure of 140,000 Pa. The liquid travels upward 6.0 m and enters a tank at a gauge pressure of 2,000 Pa. The diameter of the pipe remains constant. At what speed does the liquid enter the tank

Answer 1

v₂ = 15.24 m / s

Step-by-step explanation:

This is an exercise in fluid mechanics

Let's write Bernoulli's equation, where the subscript 1 is for the factory pipe and the subscript 2 is for the tank.

P₁ + ½ ρ v₁² + ρ g y₁ = P₂ + ½ ρ v₂² + ρ g y₂

They indicate the pressure in the factory P₁ = 140000 Pa, the velocity

v₁ = 5.5 m / s and the initial height is zero y₁ = 0

the tank is at a pressure of P2 = 2000 Pa and a height of y₂ = 6.0 m

P₁ -P₂ + ρ g (y₁ -y₂) + ½ ρ v₁² = ½ ρ v₂²

let's calculate

140,000 - 2000 + ρ 9.8 (0- 6) + ½ ρ 5.5² = ½ ρ v₂²

138000 - ρ 58.8 + ρ 15.125 = ½ ρ v2²

v₂² = 2 (138000 /ρ - 58.8 + 15.125)

v₂ =
`\sqrt{(276000)/(\rho ) - 43.675 }`

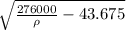
In the exercise they do not indicate what type of liquid is being used, suppose it is water with

ρ = 1000 kg / m³

v₂ =
`\sqrt{(276000)/(1000) - 43.675}`

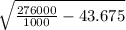
v₂ = 15.24 m / s