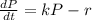Answer:
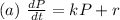
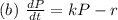
Explanation:
Given
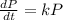
Solving (a): Differential equation for immigration where
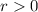
We have:
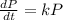
Make dP the subject
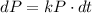
From the question, we understand that:
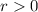 . This means that
. This means that
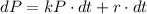 --- i.e. the population will increase with time
--- i.e. the population will increase with time
Divide both sides by dt
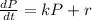
Solving (b): Differential equation for emigration where
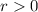
We have:
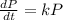
Make dP the subject
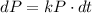
From the question, we understand that:
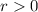 . This means that
. This means that
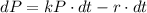 --- i.e. the population will decrease with time
--- i.e. the population will decrease with time
Divide both sides by dt