Answer:
P(X > 50.3) = 0.85
Explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:
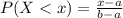
The probability of finding a value between c and d is:
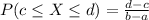
The probability of finding a value above x is:

The lengths of a professor's classes has a continuous uniform distribution between 50.0 min and 52.0 min.
This means that
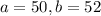
If one such class is randomly selected, find the probability that the class length is more than 50.3 min.
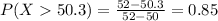
So
P(X > 50.3) = 0.85