y' + 6y = f(t)
where
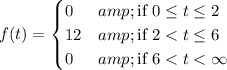
You can write f(t) in terms of the unit step (i.e. Heaviside theta) function u(t), which is defined as
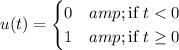
Then the DE is written as
y' + 6y = 12 u (t - 2) - 12 u (t - 6)
(a) Take the Laplace transform of both sides:
LT[y' + 6y] = LT[12 u (t - 2) - 12 u (t - 6)]
s Y - y (0) + 6Y = 12 (exp(-2s) - exp(-6s))/s
(b) Solve for Y :
(s + 6) Y = 12 (exp(-2s) - exp(-6s))/s + y (0)
Y = 12 (exp(-2s) - exp(-6s))/(s (s + 6)) + y (0)/(s + 6)
(c) Take the inverse transform:
LT⁻¹ [Y] = LT⁻¹[12 (exp(-2s) - exp(-6s))/(s (s + 6)) + y (0)/(s + 6)]
y = 12 LT⁻¹ [(exp(-2s) - exp(-6s))/(s (s + 6))] + y (0) LT⁻¹ [1/(s + 6)]
y = 12 u (t - 2) LT⁻¹ [1/(s (s + 6))] - 12 u (t - 6) LT⁻¹ [1/(s (s + 6))] + y (0) exp(-6t )
For the remaining inverse transform, break up into partial fractions:
1/(s (s + 6)) = a/s + b/(s + 6)
1 = a (s + 6) + bs
1 = (a + b) s + 6a
==> 6a = 1, a + b = 0 ==> a = 1/6, b = -1/6
y = 2 u (t - 2) LT⁻¹ [1/s - 1/(s + 6)] - 2 u (t - 6) LT⁻¹ [1/s - 1/(s + 6)] + y (0) exp(-6t )
y = 2 u (t - 2) (1 - exp(-6t )) - 2 u (t - 6) (1 - exp(-6t )) + y (0) exp(-6t )