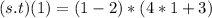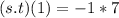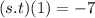Question

Suppose that the functions s and t are defined for all real numbers x as follows.

s (x)=x-2
t(x) = 4x+3
Write the expressions for (s +t)(x) and (s – t)(x) and evaluate (s.t)(1).

Answer 1

`(s + t)(x)= 5x+1`

`(s - t)(x)= -3x-5`

`(s.t)(1) = -7`

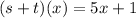
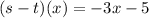
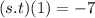
Explanation:

Given

`s(x) = x - 2`

`t(x) = 4x + 3`

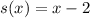
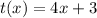
Solving (a): (s + t)(x)

This is calculated as:

`(s + t)(x)= s(x) + t(x)`

`(s + t)(x)= x-2 + 4x + 3`

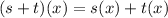
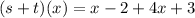
Collect like terms

`(s + t)(x)= x+ 4x-2 + 3`

`(s + t)(x)= 5x+1`

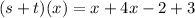
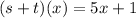
Solving (b): (s - t)(x)

This is calculated as:

`(s - t)(x)= s(x) - t(x)`

`(s - t)(x)= x-2 - 4x - 3`

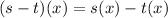
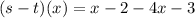
Collect like terms

`(s - t)(x)= x- 4x-2 - 3`

`(s - t)(x)= -3x-5`

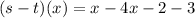
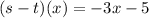
Solving (b): (s . t)(1)

First, we calculate (s.t)(x)

This is calculated as:

`(s.t)(x) = s(x)* t(x)`

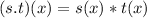
So, we have:

`(s.t)(x) = (x - 2) * (4x + 3)`

Substitute 1 for x

`(s.t)(1) = (1 - 2) * (4*1 + 3)`

`(s.t)(1) = - 1 * 7`

`(s.t)(1) = -7`