Answer:
The right answer is:
(a)
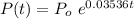
(b)
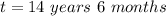
(c)
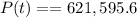 ($)
($)
Explanation:
Given:
House price increment rate,
= 3.6% annually
(a)
Let the exponential equation will be:
⇒
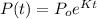
here,
t = 0
P = P₀
t = 1 yr
then,
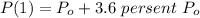
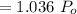
now,
⇒
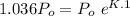
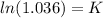
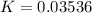
Thus, the exponential equation will be "
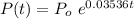 ".
".
(b)
We know,
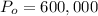 ($)
($)
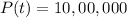 ($)
($)
∵
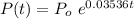
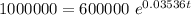
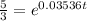

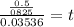
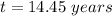
or,
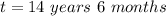
(c)
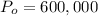 ($)
($)

Now,
⇒
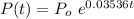
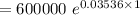
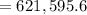 ($)
($)