Answer:
solid cylinder
Step-by-step explanation:
the object that arrives first is the object that has more speed, let's use the concepts of energy
starting point. Highest point
Em₀ = U = m g h
final point. Lowest point
Em_f = K = ½ mv² + ½ I w²
since the body has rotational and translational movement
how energy is conserved
m g h = ½ mv² + ½ I w²
linear and angular velocity are related
v = w r
w = v / r
we substitute
m g h = ½ mv² + ½ I (v/r) ²
mg h = ½ v² (m + I /r²)
v =
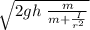
the tabulated moments of inertia for the bodies are
solid cylinder I = ½ m r²
hollow cylinder I = m r²
we look for the speed for each body
solid cylinder
v₁ =
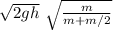
v₁ =
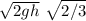
let's call v₀ =
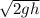
v₁ = 0.816 v₀
hollow cylinder
v₂ =

v₂ = v₀ √½
v₂ = 0.707 v₀
Therefore, the body that has the highest speed is the solid cylinder and since time is the inverse of speed, this is the body that spends less time to reach the bottom, that is, it is the first to arrive