Question

A 61.1-kg person, running horizontally with a velocity of +2.16 m/s, jumps onto a 16.1-kg sled that is initially at rest. (a) Ignoring the effects of friction during the collision, find the velocity of the sled and person as they move away. (b) The sled and person coast 30.0 m on level snow before coming to rest. What is the coefficient of kinetic friction between the sled and the snow?

Answer 1

(a) v = 1.71 m/s

(b) μ = 0.005

Step-by-step explanation:

(a)

Using the law of conservation of the momentum:

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\`

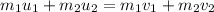
where,

m₁ = mass of person = 61.1 kg

m₂ = mass of sled = 16.1 kg

u₁ = initial speed of the person = 2.16 m/s

u₂ = initial speed of the sled = 0 m/s

v₁ = v₂ = v = final speeds of both the person and the sled = ?

Therefore,

`(61.1\ kg)(2.16\ m/s)+(16.1\ kg)(0\ m/s)=(61.1\ kg)(v)+(16.1\ kg)(v)\\\\v = (131.976\ kgm/s)/(77.2\ kg)`

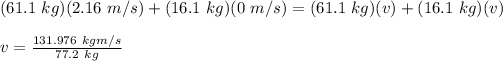
v = 1.71 m/s

(b)

The kinetic energy lost by the sled must be equal to the frictional energy:

K.E = fd

`(1)/(2)mv^2=\mu Rd = \mu Wd\\\\(1)/(2)mv^2=\mu mgd\\\\(1)/(2)v^2=\mu g\\\\\mu = (v^2)/(2gd)`

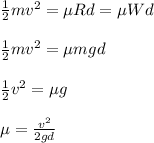
where,

μ = coefficient of kinetic friction = ?

d = distance covered = 30 m

g = acceleration due to gravity = 9.81 m/s²

Therefore,

`\mu = ((1.71\ m/s)^2)/((2)(9.81\ m/s^2)(30\ m))`

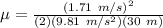
μ = 0.005