Answer:
1. 16%
2. The middle 95% of newborn babies weigh between 6.2 and 9 pounds.
3. 2.5%
4. Approximately 50% of newborn babies weigh more than 7.6 pounds.
5. 83.85%
Explanation:
The Empirical Rule states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.
Approximately 95% of the measures are within 2 standard deviations of the mean.
Approximately 99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean of 7.6 pounds, standard deviation of 0.7 pounds
1. What percent of newborn babies weigh more than 8.3 pounds?
7.6 + 0.7 = 8.3.
So more than 1 standard deviation above the mean.
The normal distribution is symmetric, which means that 50% of the measures are below the mean and 50% are above.
Of those above the mean, 100 - 68 = 32% are more than one standard deviation above the mean. So
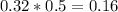
16% of newborn babies weigh more than 8.3 pounds.
2. The middle 95% of newborn babies weigh between and pounds.
Within 2 standard deviations of the mean, so:
7.6 - 2*0.7 = 6.2 pounds
7.6 + 2*0.7 = 9 pounds.
The middle 95% of newborn babies weigh between 6.2 and 9 pounds.
3. What percent of newborn babies weigh less than 6.2 pounds?
More than 2 standard deviations below the mean, which is 5% of the 50% below the mean, so:
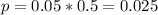
2.5% of newborn babies weigh less than 6.2 pounds.
4. Approximately 50% of newborn babies weigh more than pounds.
Due to the symmetry of the normal distribution, the mean, so 7.6 pounds.
Approximately 50% of newborn babies weigh more than 7.6 pounds.
5. What percent of newborn babies weigh between 6.9 and 9.7 pounds?
6.9 = 7.6 - 0.7
9.7 = 7.6 + 3*0.7
Within 1 standard deviation below the mean(68% of the 50% below) and 3 standard deviations above the mean(99.7% of the 50% above). So

83.85% of newborn babies weigh between 6.9 and 9.7 pounds.