Answer:
25/3 ft/s
Explanation:
Height of pole , h=15 ft
Height of man, h'=6 ft
Let BD=x
BE=y
DE=BE-BD=y-x
All right triangles are similar
When two triangles are similar then the ratio of their corresponding sides are equal.
Therefore,


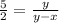
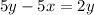
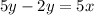
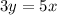
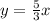
Differentiate w.r.t t

We have dx/dt=5ft/s
Using the value
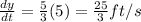
Hence, the tip of his shadow moving with a speed 25/3 ft/s when he is 45 feet from the pole.