Answer: 45 and 25
Explanation:
Given
Five years ago victor was twice as old as his daughter
Suppose the current age of victor and his daughter are x and y
For five years ago
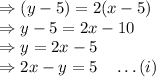
In 10 years sum of their ages is 90
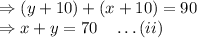
On solving (i) and (ii) we get
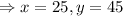
So, the current age of victor is 45 and his daughter is 25