Question

Plzzz helppp only a hour due today

Answer 1

A or C

Is my best I got stuck A or C

Answer 2

`\text{C. about }72.05\:\mathrm{cm^2}`

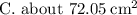
Explanation:

This is a very fun problem that requires the use of multiple concepts to solve.

Concepts/formulas used:

• The measure of an inscribed angle is half the measure of the arc it forms
• There are 360 degrees in a circle
• The sum of the interior angles of a triangle add up to 180 degrees
• Law of Sines is given by
  `(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`
• All radii of a circle are exactly half all diameters of the circle
• The area of a circle with radius
  `r` is given by
  `A=r^2\pi`

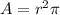
The measure of an inscribed angle is equal to half the measure of the arc it forms. In circle Z,
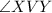`\angle XVY` is an inscribed angle that forms arc XY. Since XY is 40 degrees, angle XVY must be
`40/ 2=20^(\circ)`.

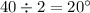Similarly,
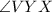`\angle VYX` is also an inscribed angle and forms arc XV. Notice how arc XY and arc XV form arc VY, which is half the circumference of the circle, since segment VY is a diameter of the circle. Since there are 360 degrees in a circle, arc VY must be 180 degrees. Therefore, we have:

`\widehat{XY}+\widehat{XV}=180^(\circ),\\\widehat{XV}+40^(\circ)=180^(\circ),\\\widehat{XV}=140^(\circ)`

Now we can find the measure of angle VYX, using our knowledge that the measure of an inscribed angle is half the measure of the arc it forms.

`m\angle VYX=(140)/(2)=70^(\circ)`

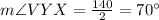
Now, we have two angles of triangle VXY. Since the sum of the interior angles of a triangle add up to 180 degrees, the third angle,
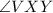`\angle VXY`, can be found:

`\angle VXY+\angle VYX+\angle XVY=180^(\circ),\\\angle VXY+20^(\circ)+70^(\circ)=180^(\circ),\\\angle VXY+90^(\circ)=180^(\circ),\\\angle VXY=90^(\circ)`

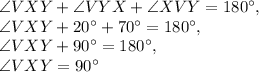
We can now use this angle and the Law of Sines to find the length of segment VY. The Law of Sines works for any triangle and is given by
`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)` (the ratio of any angle and its opposite side is maintained throughout all angles of the triangle).

Since angle VXY's opposite side is VY and angle VYX's opposite side is VX, we have the following proportion:

`(\sin 70^(\circ))/(9)=(\sin 90^(\circ))/(VY)`

Recall that
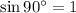`\sin 90^(\circ)=1`. Cross-multiply:

`9\sin 90^(\circ)=VY\sin 70^(\circ),\\9=VY\sin 70^(\circ),\\VY=(9)/(\sin 70^(\circ))`

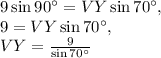
This is the diameter of the circle. By definition, all radii are half the diameter. Therefore, the radius of the circle is
`(9)/(\sin 70^(\circ))\cdot (1)/(2)=(9)/(2\sin 70^(\circ))`.

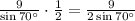The area of a circle with radius
`r` is given by
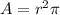`A=r^2\pi`. Substitute
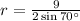`r=(9)/(2\sin 70^(\circ))` to get the area of circle Z:

`A=((9)/(2\sin 70^(\circ)))^2\pi,\\A\approx (4.78879997614)^2\pi,\\A\approx 22.9326052115\pi,\\A\approx \boxed{72.05\:\mathrm{cm^2}}`