Answer:

Explanation:
From the question we are told that:
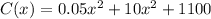
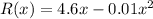
Generally the equation for Profit is is mathematically given by


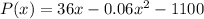
Differentiate P(x) we have
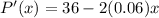
Equating to 0
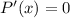

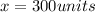
Second order differentiation, we have

Therefore
This implies that
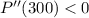
Hence, Maximum Profit is actualized at
