Answer:
0.8 = 80% probability that they did in fact study for the test.
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Passed the exam.
Event B: Studied.
Probability of passing the test:
80% of 60%(Studied).
30% of 100 - 60 = 40%(did not study). So
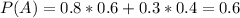
Probability of passing the test studying:
80% of 60%, so:
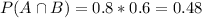
Find the probability that they did in fact study for the test with this knowledge in hand.
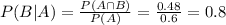
0.8 = 80% probability that they did in fact study for the test.