Question

A shopkeeper allows 15% discount on the marked price, still he manages to have 7% profit. How much high did he mark his goods above the cost price?

Answer 1

Answer:
`25.9\%`

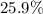
Explanation:

Given

Shopkeeper allows 15% discount on the marked price and still manages a profit of 7%

Suppose the marked price is
`x`

So, the selling price is
`(1-0.15)x=0.85x`

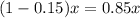
Suppose the cost price is
`y`

`\Rightarrow (0.85x-y)/(y)=7\%\\\\\Rightarrow (0.85x)/(y)-1=0.07\\\\\Rightarrow (0.85x)/(y)=1.07\\\\\Rightarrow y=(0.85x)/(1.07)\\\\\Rightarrow y=0.794x`

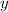
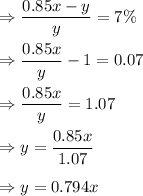
So, the percentage the shopkeeper marked his goods above cost price

`\Rightarrow (x-y)/(y)* 100\\\\\Rightarrow (x-0.794x)/(0.794)* 100\\\\\Rightarrow (0.2056)/(0.794x)* 100\\\\\Rightarrow 25.89\%\approx 25.9\%`