Answer:
7 units
Explanation:
Given
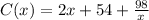
Required
The units that minimize the average cost
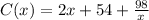
Differentiate
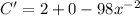

Equate to 0 to solve for x
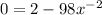
Collect like terms

Divide by 98
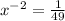
Rewrite as:
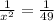
Take square roots of both sides
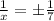
Take multiplicative inverse of both sides

Only positive value will produce critical value. Hence, 7 units will produce the minimum average cost