Answer:
All the engine fan blades must be replaced
Explanation:
From the question we are told that:
Sample size
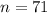
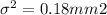
Variance
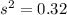
Level of significance
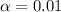
Generally the hypothesis is
The test hypothesis is
Null
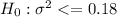
Alternative

Generally the equation for Chi distribution is mathematically given by
The test statistic is
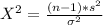
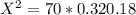
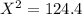
Since
Critical Value


Hence, we Reject
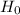 ,Given that 124.4 is Greater than 100.4252
,Given that 124.4 is Greater than 100.4252
Therefore
All the engine fan blades must be replaced