Answer:
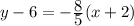
OR

Explanation:
Hi there!
Point-slope form:
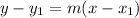 where
where
 is a point and
is a point and
 is the slope
is the slope
1) Determine the slope
 where two given points are
where two given points are
 and
and

Plug in the given points (-2, 6) and (3,-2):
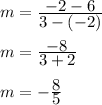
Therefore, the slope of the line is
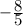 . Plug this into
. Plug this into
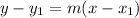 :
:
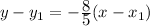
2) Plug in a point

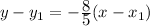
We're given two points, (-2, 6) and (3,-2), so there are two ways we can write this equation:
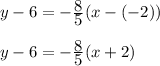
OR
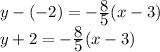
I hope this helps!