Question

Compute the standard deviation of the following set of data to the nearest whole number:

8, 12, 15, 17, 18
14
03
04
13

Answer 1

Explanation:

The standard deviation is the square root of the variance, and the variance is found by using the mean. So we will do that first. I will use the population variance as opposed to the sample variance since our set of numbers is small.

The mean: 8 + 12 + 15 + 17 + 18 = 70 and divide that by 5 to get

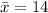`\bar{x}=14` and use this to find the variance in the formula:

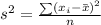`s^2=\frac{\sum(x_i-\bar{x})^2}{n}` it is a bit difficult to enter that formula in correctly, but here's how it works mathematically:

`s^2=((8-14)^2+(12-14)^2+(15-14)^2+(17-14)^2+(18-14)^2)/(5)`

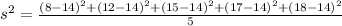
Squaring this ensures us that we don't end up with zero, which would be useless.

`s^2=(36+4+1+9+16)/(5)` so

`s^2=13.2` which means that the standard deviation is

s = 3.633

(If you do it with n-1 = 4 in the denominator of the variance, you get a standard deviation of 4.062)