Answer:
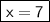
Explanation:
We are here given a logarithmic equation and we need to solve it out and then find the value of x. The given equation is ,
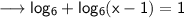
Here I am assuming that the base of the logarithm is 6 . The equation can be written as ,
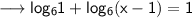
Recall the property of log as ,
 , on using this property we have ,
, on using this property we have ,
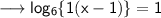
Simplify ,
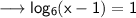
We know that , if
 then in expotential form it can be expressed as
then in expotential form it can be expressed as
 . Using this we have ,
. Using this we have ,
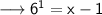
Simplify ,
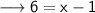
Add 1 both sides ,
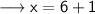
Therefore ,
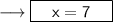
Hence the value of x is 7 .