Question

How many different license plates are possible if each contains 4 letters (out of the alphabet's 26 letters) followed by 2 digits (from 0 to 9)? How many of these license plates contain no repeated letters and no repeated digits? There aredifferent possible license plates. (Simplify your answer.) There are different possible license plates if no letters or numbers are repeated. (Simplify your answer.)

Answer 1

There are 45,697,600 different possible license plates. If no letters or numbers are repeated, there are 32,292,000 possible license plates.

Explanation:

For the first question, we can repeat letters and digits.

Let
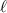`\ell` represent a letter and
`#`
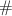`\#` represent a digit. The license plate format given is:

`\underline{\ell}\:\:\underline{\ell}\:\:\underline{\ell}\:\:\underline{\ell}\:\:\underline{n}\:\:{\underline {n}`

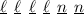
For each letter, there are 26 letters to choose from (alphabet). For each digit, there are 10 numbers to choose from (0-9).

Since we're choosing 4 letters and 2 numbers, the number of possible license plates is:

`26\cdot 26\cdot 26\cdot 26\cdot 10\cdot 10=\boxed{45,697,600}`

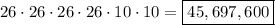
If we stipulate that no letter or digit may be repeated, then we'll still have 26 choices for the first letter, but for the second letter, we'll only have 25. Then 24, 23, and so on. Similarly, for the first digit, there will be 10 choices, then 9, 8, and so on.

Therefore, the desired answer for the second part of the question is:

`26\cdot 25\cdot 24\cdot 23\cdot 10\cdot 9=\boxed{32,292,000}`

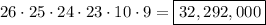
*Note that we don't need to account for rearrangements as
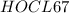`HOCL67` and
`CLHO76` are considered different license plates (order matters).