Answer:
a) Hence the probability that the average test score in the class of size 25 exceeds 80.
P ( X > 74) = 0.9838
P ( Z > 2.14) = 0.0162
b) Hence the probability that the average test score for the class of size 64
P ( X > 74) = 0.9838
P ( Z > 2.14) = 0.0003
c) Probability of the difference exceeding 2.2 = 0.9936
P (Z < 2.49) = 0.0064
Explanation:
Let's assume a normal distribution.
Now,
a) For a class of 25
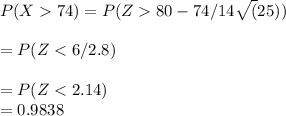
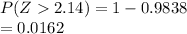
b)
Similarly:
For the class of 64

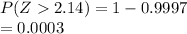
c) Probability of the difference exceeding 2.2
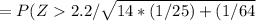
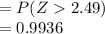
P (Z < 2.49)
= 1 - 0.9936
= 0.0064