Given:
Mark started reading on Saturday , and he is reading 40 pages per day.
Allen didn't start until Sunday , but he is still reading 45 pages a day.
To find:
How many days will it take Allen to catch up to Mark, and how many pages will they each have read?
Solution:
Let
 represent the number of days Allen has been reading. Then the number of days Mark has been reading is
represent the number of days Allen has been reading. Then the number of days Mark has been reading is
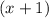 .
.
Mark is reading 40 pages per day. So, he will read
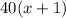 pages.
pages.
Allen is reading 45 pages a day. So, he will read
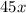 pages.
pages.
Allen catch up to Mark when they read equal number of pages.
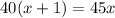
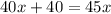
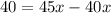
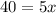
Divide both sides by 5.

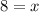
In 8 days Allen will catch up to Mark.
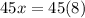

Therefore, they each have read 360 pages.