Answer:
x = 3.3
Explanation:
A equation is given to us and we need to solve out for x. The given equation is ,
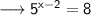
Take log on both sides with base as " 10" . We have ,

Simplify using the property of log ,
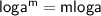 , we have ,
, we have ,

Simplify ,
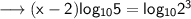
Again simplify using the property of log ,
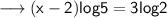
We know that log 5 = 0.69 and log 2 = 0.301 , on substituting this , we have ,
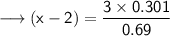
Simplify the RHS ,
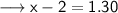
Add 2 both sides ,
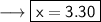
Hence the Value of x is 3.30 .