Answer:
0.735 = 73.5% probability of getting at least 4 calls between eight and nine in the morning.
Explanation:
We have the mean during a time interval, which means that the Poisson distribution is used to solve this question.
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
The number of calls received by an office on Monday morning between 8:00 AM and 9:00 AM has a mean of 5.
This means that
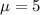
Calculate the probability of getting at least 4 calls between eight and nine in the morning.
This is:

In which
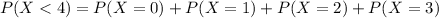
So

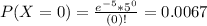
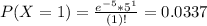
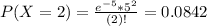
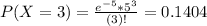
Then

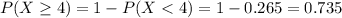
0.735 = 73.5% probability of getting at least 4 calls between eight and nine in the morning.