Answer:
the number of ways to select at least 1 democrat in the subcommittee is 69,486 ways
Explanation:
Given;
number of the subcommittee, = 6
number of democrats = 10
number of republicans, = 12
The number of ways to select at least 1 democrat in the subcommittee is calculated as follows;
Let D represent Democrats
let R represent Republicans
= (1D & 5R) or (2D & 4R) or (3D & 3R) or (4D & 2R) or (5D & 1R) or (6D)
= 10C₁ x 12C₅ + 10C₂ x 12C₄ + 10C₃ x 12C₃ + 10C₄ x 12C₂ + 10C₅ x 12C₁ + 10C₆
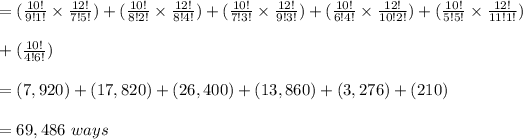
Therefore, the number of ways to select at least 1 democrat in the subcommittee is 69,486 ways