Question

A housing official in a certain city claims that the mean monthly rent for apartments in the city is less than $1000. To verify this claim, a simple random sample of 47 renters in the city was taken, and the mean rent paid was $941 with a standard deviation of $245. Can you conclude that the mean monthly rent in the city is less than $1000

Answer 1

The p-value of the test is 0.053, which is more than the standard significance level of 0.05, and thus it cannot be concluded that the mean monthly rent in the city is less than $1000.

Explanation:

A housing official in a certain city claims that the mean monthly rent for apartments in the city is less than $1000.

At the null hypothesis, we test if the mean is of at least $1000, that is:

`H_0: \mu \geq 1000`

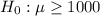
At the alternative hypothesis, we test if the mean is less than $1000, that is:

`H_1: \mu < 1000`

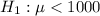
The test statistic is:

We have the standard deviation for the sample, so the t-distribution is used.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

1000 is tested at the null hypothesis:

This means that
`\mu = 1000`

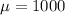
To verify this claim, a simple random sample of 47 renters in the city was taken, and the mean rent paid was $941 with a standard deviation of $245.

This means that
`n = 47, X = 941, s = 245`

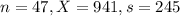
Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (941 - 1000)/((245)/(√(47)))`

`t = -1.65`

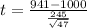
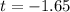
P-value of the test and decision:

The p-value of the test is found using a left-tailed test(test if the mean is less than a value), with t = -1.65 and 47 - 1 = 46 df.

Using a t-distribution calculator, the p-value is of 0.053.

The p-value of the test is 0.053, which is more than the standard significance level of 0.05, and thus it cannot be concluded that the mean monthly rent in the city is less than $1000.