Question

A survey of 77 teenagers finds that 30 have 5 or more servings of soft drinks a week. a. Give a 90% confidence interval for the proportion of teenagers who have 5 or more servings of soft drinks a week. b. In the general population, 30% have 5 or more servings of soft drinks a week. Is there evidence that a higher proportion of teenagers have 5 or more servings of soft drinks a week than the general population

Answer 1

a) The 90% confidence interval for the proportion of teenagers who have 5 or more servings of soft drinks a week is (0.2982, 0.481).

b) 30% = 0.3 is part of the confidence interval, which means that there is no evidence that a higher proportion of teenagers have 5 or more servings of soft drinks a week than the general population.

Explanation:

Question a:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

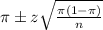
In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

A survey of 77 teenagers finds that 30 have 5 or more servings of soft drinks a week.

This means that
`n = 77, \pi = (30)/(77) = 0.3896`

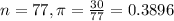
90% confidence level

So
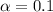`\alpha = 0.1`, z is the value of Z that has a p-value of
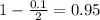`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

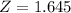The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.3896 - 1.645\sqrt{(0.3896*0.6104)/(77)} = 0.2982`

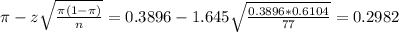
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.3896 + 1.645\sqrt{(0.3896*0.6104)/(77)} = 0.481`

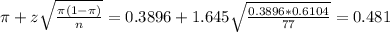
The 90% confidence interval for the proportion of teenagers who have 5 or more servings of soft drinks a week is (0.2982, 0.481).

Question b:

30% = 0.3 is part of the confidence interval, which means that there is no evidence that a higher proportion of teenagers have 5 or more servings of soft drinks a week than the general population.