Answer:
The domain and range remain the same.
Explanation:
Hi there!
First, we must determine what increasing a by 2 really does to the exponential function.
In f(x)=ab^x, a represents the initial value (y-intercept) of the function while b represents the common ratio for each consecutive value of f(x).
Increasing a by 2 means moving the y-intercept of the function up by 2. If the original function contained the point (0,x), the new function would contain the point (0,x+2).
The domain remains the same; it is still the set of all real x-values. This is true for any exponential function, regardless of any transformations.
The range remains the same as well; for the original function, it would have been
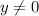 . Because increasing a by 2 does not move the entire function up or down, the range remains the same.
. Because increasing a by 2 does not move the entire function up or down, the range remains the same.
I hope this helps!