Answer:
Graph (a)
Explanation:
Given
![y = \sqrt[3]{x+ 6} -3](https://img.qammunity.org/2022/formulas/mathematics/college/m9vmatqd24bqyi0rpmw6drhuolv9rbr0go.png)
Required
The graph
First, calculate y, when x = 0
![y = \sqrt[3]{0+ 6} -3](https://img.qammunity.org/2022/formulas/mathematics/college/qmw4uns2kqtvz4wy0m71zwaw902xllcukv.png)
![y = \sqrt[3]{6} -3](https://img.qammunity.org/2022/formulas/mathematics/college/j8lg53wsmua61tumw1trr2rpjtp40ifo6q.png)
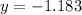
The above value of y implies that the graph is below the origin when x = 0. Hence, (c) and (d) are incorrect because they are above the origin
Also, only the first graph passes through point (0,-1.183). Hence, graph (a) is correct