Question

Find cosθ+cos3θ+cos5θ+cos7θ by using the Sum-to-Product Formula.

Please also show your work as well. Thanks!

Answer 1

`\rm\displaystyle 4\cos( \theta) \cos \left( {2\theta} \right) \cos \left( {4 \theta } \right)`

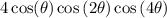
Explanation:

I assume the question want us to rewrite cosθ+cos3θ+cos5θ+cos7θ by using Sum-to-Product Formula and note that it's not an equation therefore θ can never be specified

===========================

so we want to rewrite cosθ+cos3θ+cos5θ+cos7θ by using Sum-to-Product Formula the good news is that the number of the function of the given expression is even so there's a way to do so, rewrite the expression in parentheses notation:

`\rm\displaystyle \left( \cos( \theta) + \cos(3 \theta) \right) + \left(\cos(5 \theta) + \cos(7 \theta) \right)`

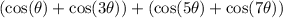
recall that,Sum-to-Product Formula of cos function:

`\rm \boxed{\displaystyle \cos( \alpha ) + \cos( \beta ) = 2 \cos \left( ( \alpha + \beta )/(2) \right) \cos \left( ( \alpha - \beta )/(2) \right) }`

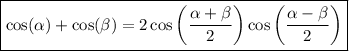
notice that we have two pair of function with which we can apply the formula thus do so,

`\rm\displaystyle \left( 2\cos \left( ( \theta + 3 \theta)/(2) \right)\cos \left( ( \theta - 3 \theta)/(2) \right) \right) + \left(2\cos \left( (5 \theta + 7 \theta)/(2) \right) \cos \left( (5 \theta - 7 \theta)/(2) \right) \right)`

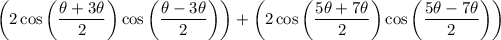
simplify addition:

`\rm\displaystyle \left( 2\cos \left( (4 \theta)/(2) \right)\cos \left( ( - 2\theta )/(2) \right) \right) + \left(2\cos \left( (12 \theta )/(2) \right) \cos \left( ( - 2 \theta)/(2) \right) \right)`

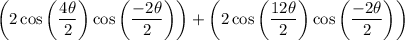
simplify division:

`\rm\displaystyle \left( 2\cos \left( {2 \theta} \right)\cos \left( { - \theta } \right) \right) + \left(2\cos \left( {6 \theta } \right) \cos \left( { - \theta} \right) \right)`

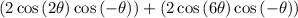
By Opposite Angle Identities we acquire:

`\rm\displaystyle \left( 2\cos \left( {2 \theta} \right)\cos \left( { \theta } \right) \right) + \left(2\cos \left( {6 \theta } \right) \cos \left( { \theta} \right) \right)`

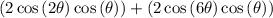
factor out 2cosθ:

`\rm\displaystyle 2 \cos( \theta) (\cos \left( {2 \theta} \right) + \cos \left( {6 \theta } \right) )`

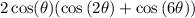
once again apply Sum-to-Product Formula which yields:

`\rm\displaystyle 2 \cos( \theta) (2\cos \left( {4\theta} \right) \cos \left( {2 \theta } \right) )`

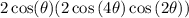
distribute:

`\rm\displaystyle 4\cos( \theta) \cos \left( {2\theta} \right) \cos \left( {4 \theta } \right)`

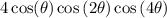
and we're done!