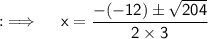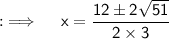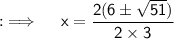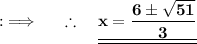Question

Solve for x: -3(x-2)^2 + 17 =0

Answer 1

Before doing the question, let's recall the quadratic formula which is used to find the roots of a quadratic equation ;

For any quadratic equation of the form ax² + bx + c = 0 , it's roots are given by the quadratic formula as :

• 
  `{\boxed{\bf{x=(-b\pm √(D))/(2a)}}}`

Where , D = b² - 4ac (Discriminant)

Now , simplifying the equation :

`{:\implies \quad \sf -3\{(x)^(2)+2^(2)-2* 2* x\}+17=0\quad \qquad \{\because (a-b)^(2)=a^(2)+b^(2)-2ab\}}`

`{:\implies \quad \sf -3(x^(2)+4-4x)+17=0}`

`{:\implies \quad \sf -3x^(2)-12+12x+17=0}`

`{:\implies \quad \sf -3x^(2)+12x+5=0}`

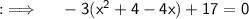
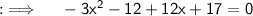
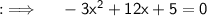
Dividing both sides by -1 will yield :

`{:\implies \quad \sf 3x^(2)-12x-5=0}`

Now , it's in the form of the standard quadratic equation , where a = 3 , b = -12 , c = 5 , and D = (-12)² - 4 × 3 × -5 = 144+60 = 204

Now, By quadratic Formula ;

`{:\implies \quad \sf x=(-(-12)\pm √(204))/(2* 3)}`

`{:\implies \quad \sf x=(12\pm 2√(51))/(2* 3)}`

`{:\implies \quad \sf x=\frac{\cancel{2}(6\pm √(51))}{\cancel{2}* 3}}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{x=(6\pm √(51))/(3)}}}`