Question

Write an equation for a parabola with endpoints of the latus rectum at (-2, 3) and (-2, 15) and the directrix at x = 4.

Answer 1

Given:

The endpoints of the latus rectum at (-2, 3) and (-2, 15).

The directrix at x = 4.

To find:

The equation of the parabola.

Solution:

The equation of the parabola is:

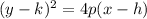`(y-k)^2=4p(x-h)` ...(1)

Where,
`x=h-p` is directrix and
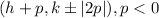`(h+p,k\pm |2p|),p<0` are the end point of the latus rectum.

The directrix at x = 4. So,

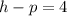`h-p=4` ...(i)

The endpoints of the latus rectum at (-2, 3) and (-2, 15). So,

`(h+p,k-|2p|)=(-2,3)`

`(h+p,k+|2p|)=(-2,15)`

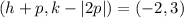
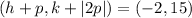
Now,

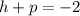`h+p=-2` ...(ii)

`k-2p=3` ...(iii)

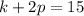`k+2p=15` ...(iv)

Adding (i) and (ii), we get

`2h=2`

`h=1`

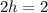
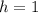
Putting
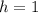`h=1` in (i), we get

`1-p=4`

`-p=4-1`

`-p=3`

`p=-3`

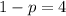
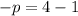
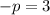
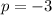
Putting
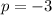`p=-3` in (iii), we get

`k-|2(-3)|=3`

`k-6=3`

`k=3+6`

`k=9`

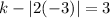
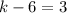
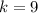
Putting
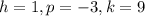`h=1,p=-3,k=9` in (1), we get

`(y-(9))^2=4(-3)(x-1)`

`(y-9)^2=-12(x-1)`

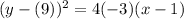
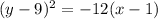
Therefore, the required equation of the parabola is
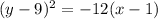`(y-9)^2=-12(x-1)`.