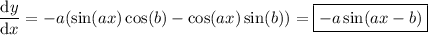Question

Find the derivative of y = cos(ax - b) from the first princip?​

Answer 1

Recall that

sin(x ± y) = sin(x) cos(y) ± cos(x) sin(y)

cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y)

Then

cos(ax - b) = cos(ax) cos(b) + sin(ax) sin(b)

When you differentiate y with respect to x, you only need to focus on the the cos(ax) and sin(ax) terms.

We have

`y = \cos(ax-b)`

`\displaystyle(\mathrm dy)/(\mathrm dx) = \cos(b)\lim_(h\to0)\frac{\cos(a(x+h))-\cos(ax)}h + \sin(b)\lim_(h\to0)\frac{\sin(a(x+h))-\sin(ax)}h`

`\displaystyle(\mathrm dy)/(\mathrm dx) = \cos(b)\lim_(h\to0)\frac{\cos(ax+ah)-\cos(ax)}h + \sin(b)\lim_(h\to0)\frac{\sin(ax+ah)-\sin(ax)}h`

`\displaystyle(\mathrm dy)/(\mathrm dx) = \cos(b)\lim_(h\to0)\frac{\cos(ax)\cos(ah)-\sin(ax)\sin(ah)-\cos(ax)}h \\+ \sin(b)\lim_(h\to0)\frac{\sin(ax)\cos(ah)+\cos(ax)\sin(ah)-\sin(ax)}h`

`\displaystyle(\mathrm dy)/(\mathrm dx) = \cos(b)\lim_(h\to0)\frac{\cos(ax)(\cos(ah)-1)-\sin(ax)\sin(ah)}h \\\\+ \sin(b)\lim_(h\to0)\frac{\sin(ax)(\cos(ah)-1)+\cos(ax)\sin(ah)}h`

`\displaystyle(\mathrm dy)/(\mathrm dx) = \cos(ax)\cos(b)\lim_(h\to0)\frac{\cos(ah)-1}h\\\\-\sin(ax)\cos(b)\lim_(h\to0)\frac{\sin(ah)}h\\\\ + \sin(ax)\sin(b)\lim_(h\to0)\frac{\cos(ah)-1}h\\\\+\cos(ax)\sin(b)\lim_(h\to0)\frac{\sin(ah)}h`

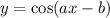
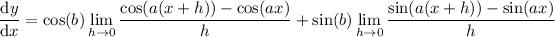
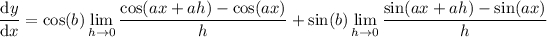
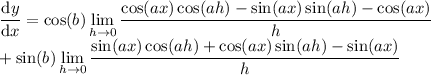
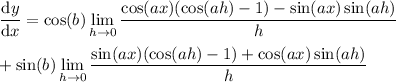
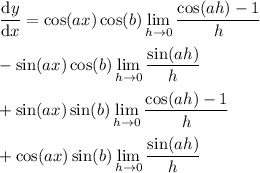
Now, recall these useful known limits: for c ≠ 0,

`\displaystyle\lim_(x\to0)(\sin(cx))/(cx)=1\text{ and }\lim_(x\to0)(1-\cos(cx))/(cx)=0`

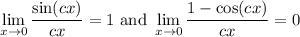
Then the limits involving cosine vanish, and the derivative simplifies to

`\displaystyle(\mathrm dy)/(\mathrm dx) = -\sin(ax)\cos(b)\lim_(h\to0)\frac{\sin(ah)}h +\cos(ax)\sin(b)\lim_(h\to0)\frac{\sin(ah)}h`

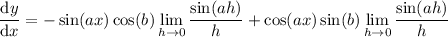
For the remaining limits, introduce a factor of a in the denominators:

`\displaystyle(\mathrm dy)/(\mathrm dx) = -a\sin(ax)\cos(b)\lim_(h\to0)(\sin(ah))/(ah) + a\cos(ax)\sin(b)\lim_(h\to0)(\sin(ah))/(ah)`

`\displaystyle(\mathrm dy)/(\mathrm dx) = -a\sin(ax)\cos(b) + a\cos(ax)\sin(b)`

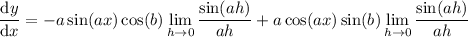
and using the first identity listed above, we can write this as

`\displaystyle(\mathrm dy)/(\mathrm dx) = -a(\sin(ax)\cos(b) - \cos(ax)\sin(b)) = \boxed{-a\sin(ax-b)}`