Answer:

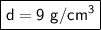
Step-by-step explanation:
1. Volume
First, we must find the cube's volume. The volume is the amount of space an object takes up. The formula for a rectangular prism's volume is length times width times height. Since a cube has equal sides, it is simply the side length cubed.
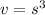
The cube has a side length of 2.0 centimeters on each side.
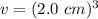
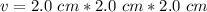
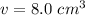
2. Density
Next, we must find the cube's density. The density is the mass per unit volume. The formula is mass over volume.
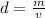
The mass of the cube is 72 grams and we just calculated the density to be 8.0 cubic centimeters.
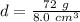
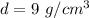
The volume of the cube is 8 cubic centimeters and the density is 9 grams per cubic centimeters.