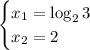Answer:
A&D
Explanation:
we want to solve the following equation for x:
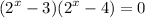
to do so let
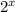 be u and transform the equation:
be u and transform the equation:
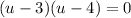
By Zero product property we obtain:
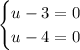
Solve the equation for u which yields:
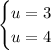
substitute back:
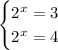
take logarithm of Base 2 in both sides of the both equations:
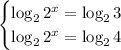
hence,