Question

See screenshot below​

Answer 1

`\displaystyle B) {x} = \log_(6) 118`

Explanation:

we would like to solve the following exponential equation:

`\displaystyle 2 \cdot {6}^(x) = 236`

to do so divide both sides by 2 which yields:

`\displaystyle {6}^(x) = 118`

take log of base 6 in both sides so that we can solve the equation for x by using
`\log_ab^c=c\log_ab` and that yields:

`\displaystyle \log_(6) {6}^(x) = \log_(6) 118`

use the formula:

`\displaystyle {x} = \log_(6) 118`

hence,

our answer is B)

Answer 2

`\boxed{\sf Option \ B }`

Explanation:

A equation is given to us and we need to find out the value of x . The given equation is ,

`\sf\dashrightarrow 2 * 6^x = 236`

Transpose 2 to RHS , we have ,

`\sf\dashrightarrow 6^x = (236)/(2)`

Simplify ,

`\sf\dashrightarrow 6^x =118`

Use log both sides with base "6"

`\sf\dashrightarrow log_6 ( 6^x) = log_6 118`

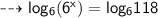
Using the property of log ,

`\sf\longmapsto \bigg\lgroup \red{\bf log_p q^r = r log_p q}\bigg\rgroup`

`\sf\dashrightarrow x \ log_6 6 = log_6 118`

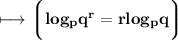
Again we know that ,

`\sf\longmapsto \bigg\lgroup \red{\bf log_p p= 1}\bigg\rgroup`

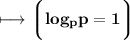
We have ,

`\sf\dashrightarrow x * 1 = log_6 118`

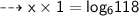
Therefore ,

`\sf\dashrightarrow\boxed{\blue{\sf x = log_6 118 }}`

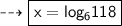
Hence option B is correct .